Выражения с несколькими переменными
Стратегии вычисления выражений с несколькими переменными являются наиболее крупными блоками для построения общей системы обработки запросов. Существуют два основных подхода, называемые параллельной обработкой и пошаговым сокращением (stepwise reduction).
Параллельная обработка компонентов запроса служит для того, чтобы избегать повторяющихся обращений к одним и тем же данным. Повторяющихся обращений к одним и тем же данным можно избежать путем одовременного вычисления нескольких компонентов запроса. В Palerno [Palermo 1972] все одноместные термы, связанные с некоторой переменной, полностью вычисляются, и все двухместные термы, в которых встречается та же переменная, частично обрабатываются одновременно путем сканирования отношения области определения этой переменной. В параллель можно вычислять даже связки через AND между термами, что еще больше сокращает размер промежуточных результатов [Jarke and Schmidt 1982]. Аналогичные подход на более высоком уровне описан в [Klug 1982b]; в этом подходе в параллель вычисляются агрегатные функции и сложные подзапросы. Стратегии планирования для параллельной обработки компонентов запросов обсуждаются Шмидтом в [Schmidt 1979].
Другим подходом, использующим преимущества параллельной обработки, являются конвейерные операции, которые могут работать с частичными результатами предыдущих операций [Smith and Chang 1975; Yao 1979]. Например, ограничение и проекция могут конвейеризоваться, так что требуется только относительно небольшой буфер для обмена данными, а не создание и последующее чтение, возможно, большого временного отношения.
Аспекты одновременного вычисления и конвейеризации объединяются в так называемом методе "обратной связи" ("feedback" method) [Clausen 1980; Rothnie 1974, 1975], в котором частичные результаты операции соединения используются для ограничения ее входных данных. То, в какой степени это можно проделать, зависит от квантификации переменных, содержащихся в соединительном терме. Например, рассмотрим выражение
[ EACH rl IN rel1: ALL rel2 IN rel2 (rl.A op rel2.B)].
Предположим, что соединительный терм вычисляется методов вложенной итерации. Пусть при проверке некоторого элемента rl обнаруживается, что терм "rl.A op rel2.B" вычисляется в false для некоторого rel2 с rel2.B = c1. Поскольку rel2 связана квантором существования, rl отвергается, и к выражению выборки может быть добавлен исключающий фильтр
[EACH rl IN rel1: NOT (rl.A op cl) AND ALL rel2 IN rel2 (rl.A op rel2.B)],
поскольку одно и то же значение rel2 вызвало бы отклонение всех элементов rl из "rel2", которые не удовлетворяют первому терму. С другой стороны, если rl с rel1.A = c2 проходит проверку, к предикату выборки можно добавить фильтр "истинности":
[EACH rl IN rel1: rl.A op c2 OR NOT (rl.A op cl) AND ...].
Оба фильтра впоследствии могут обновляться для усиления ограничений.
Второй подход к вычислению выражения с несколькими переменными обосновывается посредством следующего примера: Пример 4.1. На рис. 6 показан объектный граф, представляющий выражение
[<d.dname> OF EACH d IN departments: SOME e IN employees(e.status = professor AND e.city = d.city) AND SOME l IN lectures (l.daytime > 8 pm AND l.dname = d.dname)]
Выражения, подобные приведенному в Примере 4.1, называются древовидными выражениями [Goodman and Shmueli 1982; Shmueli 1981], поскольку ассоциированный с ними граф является деревом. Стандартный подход к вычислению такого выражения состоял бы в формировании соединения всех трех отношений, ограничении промежуточного результата в соответствии с одноместными термами и заключительной проекции на атрибуты, указанные в целевом списке. Как показано во вводном примере (разд. 1.2, стратегия 2), этот метод выполняется довольно плохо. Это еще более проблематично в распределенной среде, где каждое отношение располагается в своем узле, и нужно передавать из узла в узел отношения целиком. Более того, отношение в целевом узле может быть временно расширенным для формирования соединения, хотя окончательный результат представляет всего лишь его горизонтальное и вертикальное подмножество.
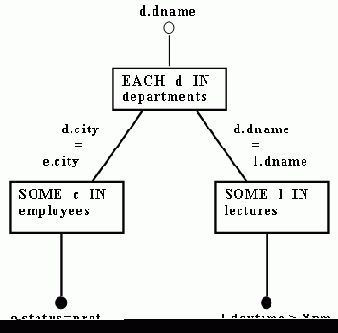
Рис. 6. Объектный граф для Примера 4.1
В [ Bernstein and Chiu 1981, Bernstein et al. 1981 и Bernstein and Goodman 1981a, 1981b, 1981c] предлагается пошаговое сокращение древовидных выражений (со свободными перемеными и переменными, связанными квантором существования). Это метод часто превосходит по производительности описанный выше простой подход, как в децентрализованных, так и централизованных средах. Он основывается на модифицированной операции соединения, и в нем используется так называемая операция полусоединения.
Полусоединение отношения "rel1" с отношением "rel2" равняется соединению этих отношений, спроецированному на атрибуты отношения "rel1":
semijoin(rel1, A op B, rel2) = proj(join(rel1, A op B, rel2), attributes rel1)).
Таким образом, эта операция формирует "половину соединения". Основные премущества полусоединения над соединением состоят в следующем: (1) для его вычисления требуется передача только списка значений атрибутов соединения вместо отношения целиком, и (2) оно обладает эффектом "сокращения", поскольку результат semijoin(rel1, A op B, rel2) всегда является подмножеством rel1, тогда как соединение в худшем случае может производить декартово произведение. Как обсуждалось в разд 4.2, в терминах реляционного исчисления полусоединение соответствует выражению с двумя переменными, где одна переменная связана квантором существования.
Простейшее вычисление древовидного выражения средствами пошагового сокращения можно описать следующим образом. Начиная с листьев дерева запроса, представляющего выражение, выполняется по одному полусоединению на каждую дугу в порядке обхода дерева в ширину от листьев к корню. Таким образом, выражение, содержащее одну свободную переменную и n-1 переменных, связанных квантором существования, может быть полностью обработано за n-1 полусоединение.
Если все переменные являются свободными, должна выполняться дополнительная последовательность полусоединений в обратном порядке.
В централизованной среде этот вид стратегии полусоединений уступает операции соединения слиянием. Объединенной с параллельным вычислением кванторов. Даже в распределенной системе простая последовательность "снизу-вверх/сверху-вниз" часто оказывается менее эффективной, чем последовательность "с середины" (middle-out), которая начинается с полусоединений с очень сильным сокращением [Chiu and Ho 1980; Chiu et al. 1981].
В стратегиях вычисления древовидных выражений, содержащих и кванторы существования, и кванторы всеобщности, необходимо учитывать порядок, в котором кванторы появляются в выражении. Пошаговое сокращение возможно только в тех случаях, когда обработка дуг в дереве запросов (в ширину, от листьев к корню) соответствует порядку кванторов в выражении (слева направо).
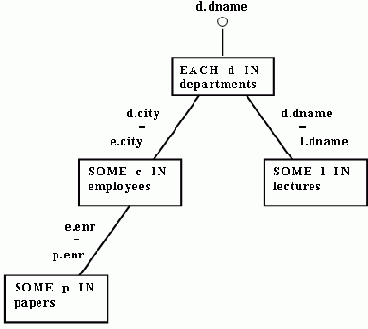
Рис. 7. Объектный граф для Примера 4.2
Пример 4.2. Рассмотрим дерево запроса на рис. 7, соответствующее выражению
[(d.dname) OF EACH d IN departments: ALL p IN papers SOME e IN employees (p.enr = e.enr AND e.city = d.city) AND SOME 1 IN lectures (1.dname = d.dname)]
Обработка этого дерева в порядке обхода в ширину от листьев к корню привела бы к получению значения выражения
[<d.dname> OF EACH d IN departments: SOME e IN employees ALL p IN papers (p.enr = e.enr AND e.city = d.city) AND SOME l IN lectures (l.dname = d.dname)],
которое не является эквивалентным исходному выражению.
Кванторы существования и всеобщности нельзя менять местами без изменения смысла выражения за исключением случаев, в которых применимы правила Q1-Q4 из таб. 1. В выражениях, содержащих только один тип кванторов, допускается произвольное изменение последовательности переменных в соответствии с правилами преобразования Q5 и Q6. Ярке и Кох [Jarke and Koch 1983] описывают направленный, так называемый "квант-граф" (quant graph), который поддержиавает применение этих правил.
Циклические выражения являются дополнением древовидных выражений по отношению ко всему множеству выражений. Хотя мы приводили некоторые исключения в разд. 3.3, в общем случае циклические выражения не могут быть полностью сокращены посредством полусоединений [Bernstein and Goodman 1981a, 1981b; Goodman and Shmueli 1982]. Пример 4.3. Рассмотрим запрос: "Названия отделов, в которых предлагаются лекции после 8 часов вечера, читаемые профессорами, проживающими в том же городе, где находится отдел".
Соответствующие выражение реляционного исчисления и граф запроса показаны на рис. 8.
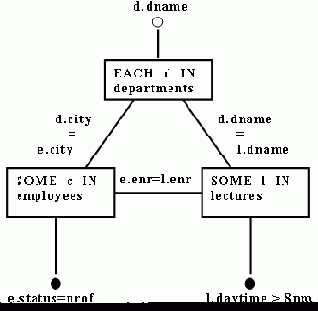
Рис 8. Циклическое выражение исчисления и соответствующий ему объектный граф
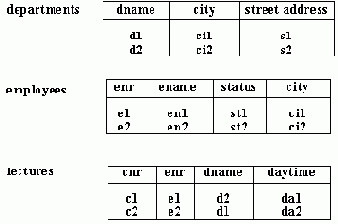
Рис 9. Некоторое возможное состояние базы данных
Если база даных находится в состоянии, показанном на рис. 9, никакая последовательность полусоединений (соответствующих дугам графа запроса с рис. 8) не произведет правильного результата (пустое отношение). Причина состоит в том, что в методе полусоединений в каждый момент времени рассматривается только одна дуга, и за счет этого теряются ограничительные условия, введенные на основе эффекта обратной связи цикла:
[(d.dname) OF EACH d IN departments: SOME e IN employees (e.status = professor AND SOME l IN lectures (l.daytime > 8 pm AND d.dname = l.dname AND l.enr = e.enr AND e.city = d.city))]
В [Kambayashi et al. 1982] предлагается обобщить применимость метода полусоединений к циклическим выражениям. Общая идея состоит в преобразовании циклического графа запроса в дерево путем добавления соответствующих термов к дугам графа. На рис. 10 демонстрируется этот метод, примененный к циклическому выражению из Примера 4.3.
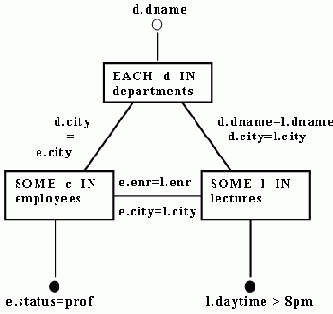
Рис 10. Дополненный объектный граф для Примера 4.3
Дополнительные термы "d.city = 1.city" и "l.city = e.city" влекут условие "d.city = e.city" по транзитивности. Таким образом, результирующий граф эквивалентен "цепочному" запросу (chain query), частной форме древовидного запроса. Заметим, что это добавление новых термов, по существу, соответствует добавлению в схему отношения "lectures" атрибута "city" (инициализированного неопределенным значением).
Затем дерево запроса обрабатывается пошаговым сокращением с выполнением обобщенного полусоединения для каждой дуги (с учетом заново введенного атрибута). Число пересылок данных сокращается за счет использования специальных методов сжатия.
Методы эффективной реализации операций, подобные представленным в этом разделе, являются кандидатами на роль компонентов аппаратуры специализированных машин баз данных.Однако в таких компонентах часто допускается параллелизм и, следовательно, требуются несколько иные алгоритмы соединений и полусоединений [Bitton et al. 1983; Maekawa 1982; Missikoff and Scholl 1983; Valduriez 1982; Valduriez and Gardarin 1984]. Краткий обзор аппаратных подходов к оптимизации запросов представлен в разд. 6.3.