Выражения с двумя переменными
Выражения с двумя переменными описывают условия для комбинации элементов из двух отношений. Вообще говоря, выражения с двумя переменными составляются из одноместных термов, ограничивающих одиночные переменные независимо одна от другой, и двухместные термы, утанавливающие связь между обоими переменными. В этом разделе мы сначала описываем базовые методы вычисления одиночного двухместного терма, соответствующего операции соединения в разд. 2.2, а затем стратегии вычисления произвольных выражений с двумя переменными.
Подходы к реализации операции соединения можно классифицировать на стратегии, зависящие от порядка, и стратегии, не зависящие от порядка [Todd 1974]. Простым методом, не зависящим от порядка доступа к элементам, является так называемый метод вложенной итерации (nested iteration) [Pecherer 1975, 1976; Selinger et al. 1979], в котором считывается каждая пара элементов отношений, и эта пара конкатенируется, если удовлетворяется условие соединения. Набросок алгоритма выглядит следующим образом:
FOR i := 1 TO N1 DO read ith element of rel1; FOR j := 1 TO N2 DO read jth element of rel2; form the join according to the join condition; END; END;
Пусть N1(N2) - число элементов отношения, считываемых во внешнем (внутреннем) цикле. Для вычисления двухместного терма требуется N1 + N1 * N2 обращений ко вторичной памяти, если считать, что для каждого элемента требуется обращение ко вторичной памяти.
Метод вложенной итерации может быть дополнен использованием индекса на атрибуте(ах) отношения "rel2". Вместо последовательного сканирования каждого элемента "rel2" для каждого элемента "rel1" парные элементы "rel2" выбираются напрямую [Griffeth 1978; Klug Klug 1982b]. Таким образом, требуется всего N1 + N1 * N2 * j12 обращений, где j12 - коэффициент селективности, характеризующий сокращение декартова произведения "rel1" и "rel2" в соответствии с условием соединения.
В методе вложенных блоков (nested block method) [Kim 1980] метод вложенной итерации адаптируется к среде страничной памяти.
Предполагается, что в буфере основной памяти будет храниться по одной или более страниц каждого отношения, и в каждой странице содержится набор записей.
Сам алгоритм в основном идентичен алгоритму, применяемому в методе вложенной итерации, за ислючением того, что считываютмя страницы памяти, а не одиночные элементы отношений. Число обращений ко вторичной памяти, требуемых для выполнения соединения, сокращается до P1 + (P1/B1) * P2, где P1(P2) - это число страниц, занимаемых внешнем (внутренним) отношением, и B1 - это число страниц внешнего отношения, удерживаемых в буфере основной памяти. Формула показывает, что во внешнем цикле всегда выгоднее считывать меньшее отношение (т.е. делать P1 < P2). Заметим, что если одно из отношений может целиком удерживаться в буфере основной памяти, то требуется P1 + P2 обращений.
Метод слияния (merge method) [Blasgen and Eswaran 1977; Selinger et al. 1979] основывается на порядке, в котором производится доступ к элементам отношения. Оба отношения сортируются в порядке возрастания или убывания значений атрибутов соединения, и производится слияние в соответствии с условием соединения. Требуется приблизительно N1 + N2 + S1
+ S2 обращений к вторичной памяти, где S1 и S2 обозначают число обращений к вторичной памяти, требуемых для сортировки обоих отношений. Если оба отношения уже отсортированы в соответствии с тем же критерием, то метод слияние выглядит наиболее эффективным методом вычисления двуместных термов [Merrett 1981; Merrett et al. 1981]. Исключениями являются те случаи, когда оба отношения достаточно малы, чтобы поместиться в основной памяти, (в этом случае предпочтительнее метод вложенных блоков), и когда одно отношение гораздо больше другого, и возможно использование индексов (в этом случае лучше работает вложенная итерация с использованием индексов).
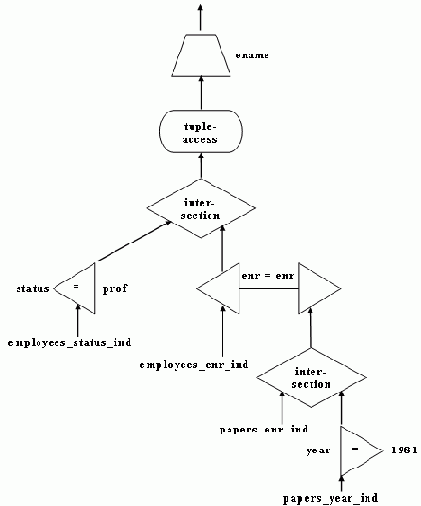
Рис 5. Граф операций, иллюстрирующий вычисление запроса из Примера 2.1.
Предполагается наличие различных индексов
Методы вычисления произвольных выражений с двумя переменными создаются на основе стратегий для выражений с одной переменной и алгоритмов вычисления двухместных термов.
Они различаются способами использования и даже создания путей доступа, таких как индексы и сортировка, и порядком обработки термов. Один из таких методов иллюстрируется на рис. 5. В нем широко используются индексы. Идентификаторы кортежей, получаемые при обработке одноместных термов, и те, которые удовлетворяют условию соединения, пересекаются и затем используются для доступа к элементам отношений. Эти элементы проецируются на атрибуты, встречающиеся в двухместных термах и целевом списке. Спроецированные элементы конкатенируются и в заключение проецируются на целевой атрибут.
В [Blasgen and Eswaran 1976, Niebuhr and Smith 1976, Yao and DeJong 1978 и 1979] описываются разнообразные другие алгоритмы и приводится их систематическое сравнение в отношении эффективности. Эти результаты демонстриуют, что часто не существует априорно лучший алгоритм. Оптимизатор должен либо полагаться на эвристики, либо производить дорогостоящее сравнение стоимости многих альтернатив для каждого запроса.
Важным случаем выражений с двумя переменными являются соединения, в которых одна из участвующих переменных ("внутренняя") связана квантором существования или всеобщности. Результат такого выражения содержит только элементы одного отношения. Кроме того, доступ к другому отношению требуется только для того, чтобы установить, удовлетворяется ли условие соединения для данного значения "внешней" переменной каким-либо элементом (соответственно, всеми элементами) отношения области определения "внутренней" переменной. Сами элементы не представляют интереса. Это означает, что для вычисления квантифицированных запросов промежуточные результаты можно представлять в сжатой форме [Dayal 1983a; Jarke and Schmidt 1981]. Если в выражении с двумя переменными содержится только один соединительный терм с операцией сравнения <, d ,>, или e, то требуется только одно значение атрибута (минимальное или максимальное значение атрибута внутреннего отношения). Тем самым, квантифицированное выражение с двумя атрибутами может быть преобразовано к одноместному терму [Jarke and Koch 1983].Кстати, аналогичное использование агрегатных функций (максимума и минимума) предлагается в контексте поддержания целостности [Bernstein et al. 1980].